余弦定理公式（
一、两角和与差的正弦、余弦、正切公式


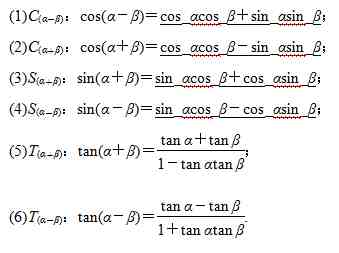
典型例题1：


两角和与差的三角函数公式可看作是诱导公式的推广 ， 可用、的三角函数表示的三角函数 ， 在使用两角和与差的三角函数公式时 ， 特别要注意角与角之间的关系 ， 完成统一角和角与角转换的目的．
二、
1：二倍角的正弦、余弦、正切公式


典型例题2：


运用两角和与差的三角函数公式时 ， 不但要熟练、准确 ， 而且要熟悉公式的逆用及变形 ， 如tan ＋tan ＝tan(＋)(1－tan tan )和二倍角的余弦公式的多种变形等．
三、两角和与差的三角函数公式的理解：
(1)正弦公式概括为“正余 ， 余正符号同”．“符号同”指的是前面是两角和 ， 则后面中间为“＋”号；前面是两角差 ， 则后面中间为“－”号．
(2)余弦公式概括为“余余 ， 正百思特网正符号异”．
(3)二倍角公式实际就是由两角和公式中令＝所得．特别地 ， 对于余弦：cos 2＝cos2－sin2＝2cos2－1＝1－2sin2 ， 这三个公式各有用处 ， 同等重要 ， 特别是逆用即为“降幂公式” ， 在考题中常有体现．
重视三角函数的“三变”：“三变”是指“变角、变名、变式”；变角为：对角的分拆要尽可能化成已知角、同角、特殊角；变名：尽可能减少函数名称；变式：对式子变形一般要尽可能有理化、整式化、降低次数等．在解决求值、化简、证明问题时 ， 一般是观察角度、函百思特网数名、所求(或所证明)问题的整体形式中的差异 ， 再选择适当的百思特网三角公式恒等变形．
典型例题3：


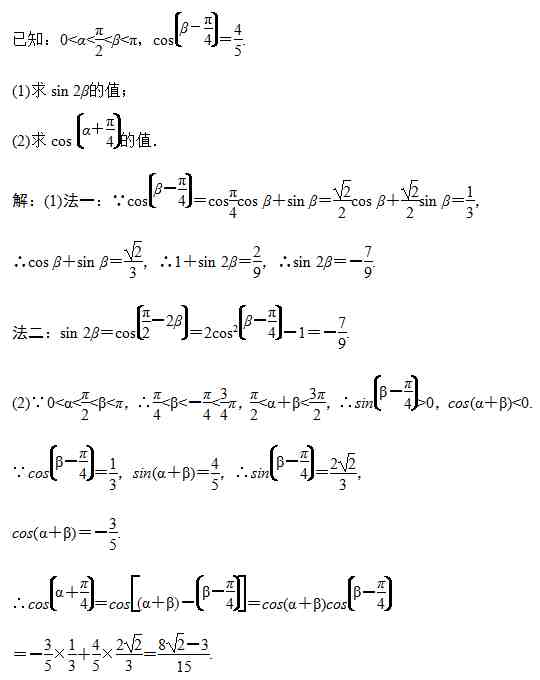
特别提醒：
1．当“已知角”有两个时 ， 一般把“所求角”表示为两个“已知角”的和或差的形式；
2．当“已知角”有一个时 ， 此时应着眼于“所求角”与“已知角”的和或差的关系 ， 然后应用诱导公式把“所求角”变成“已知角”．
3．常见的配角技巧：

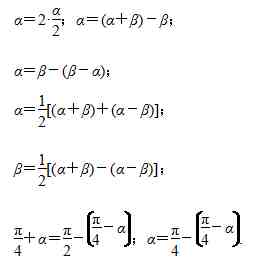
【作者：吴国平】