扫雷攻略|玩扫雷还有什么技巧？( 三 ) 「问人人知识网」

很不幸，求解一个扫雷游戏的解，正好是一个 NP 完全问题——在能够轻松验证结果是否正确的问题里面最难的那一类。这一类问题目前为止人们还没有发现多项式时间的求解算法，通常只有指数级甚至阶乘级的搜索算法来解决。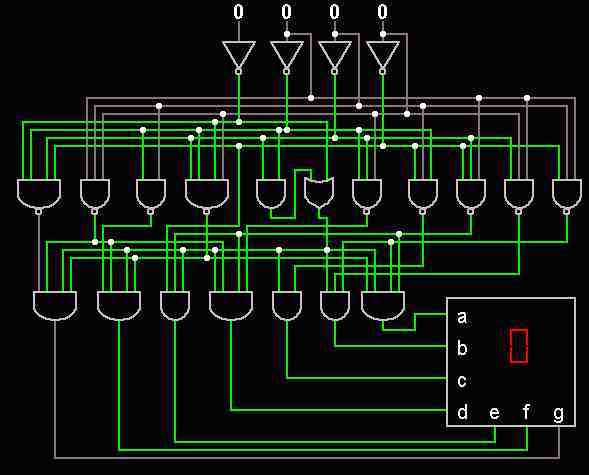

用来显示液晶数字的逻辑电路。我们可以很方便地一个一个试，但是反过来却很难，尤其是在这个逻辑电路非常庞大的时候
扫雷游戏属于一个如此困难的问题，其原因就出在上一章提到的，可以把扫雷游戏看做一个个逻辑门进行运算的逻辑电路。给定一个逻辑电路，在已知输出结果的情况下，能否确定每个输入的值？这个问题被称为 SAT 问题，是世界上第一个被证明其为 NP 完全的问题。[8]这种问题验证起来非常容易，你只需要把结果代入到逻辑电路中，马上能知道是否符合要求，但倒过来想要计算符合结果的输入就极端地麻烦。
求解扫雷游戏的结果，利用那些构造的逻辑门，恰恰等价于求解 SAT 问题。[9]
扫雷还和渗透有关系
Precolation

液体，图片来自 Giphy，Michael Shillingburg
其实我们在玩扫雷游戏的时候觉得很难，其实还有另外一个原因。这个原因和物理里面的渗透还有关系。
在上个世纪 60 年代，科学家们 [10] 发现在流体流过多孔的介质的时候，介质中的空洞总是会被堵塞，有时候就会影响流体流出。更为奇怪的是，当这些多孔的介质的孔隙被随机堵塞的比例逐渐增大而达到某一值时，一开始一直能够流动的流体就突然被完全堵住。在孔洞被随机堵住的概率发生变化时，液体流过的比率也会发生一个突变。
这种现象被称为逾渗（precolation）。[11]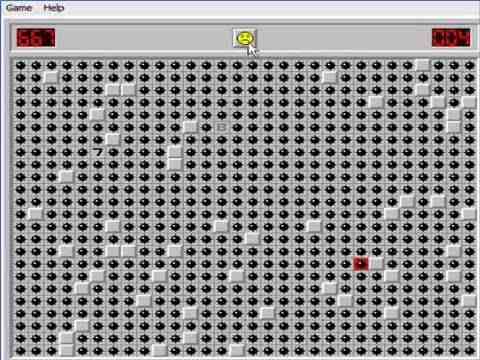

遇到这种情况，你该怎么下手
在扫雷里面，也存在类似逾渗的现象。当一盘游戏里面的地雷密度特别低的时候，我们差不多随便点，都不会点到地雷，而是点到大片大片的空白，一下子就把问题解决了。但是当地雷密度增高以后，在增大到一定程度以后，即使我们理性地分析，从不瞎猜，也不可能把扫雷问题做对了。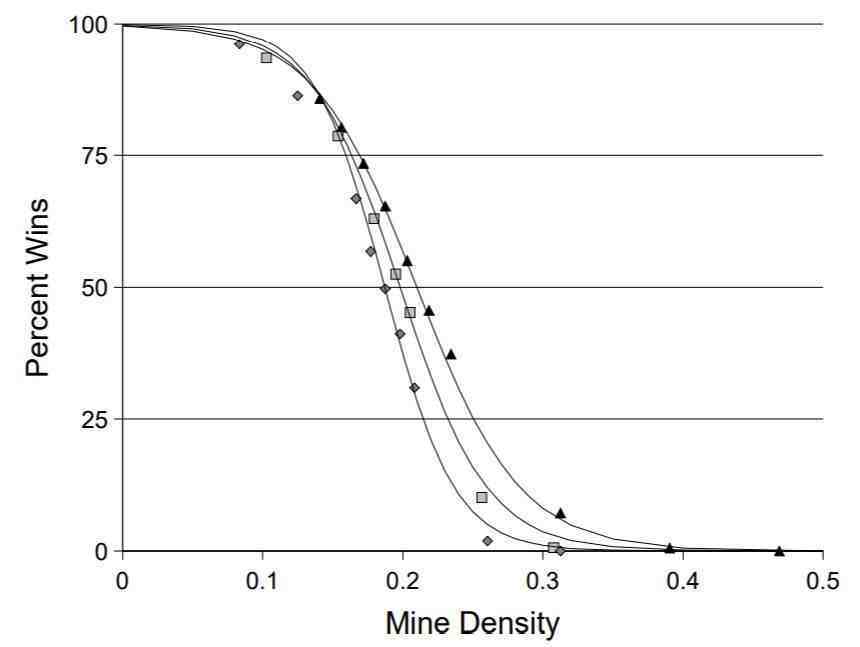

针对不同的棋盘大小，有人计算了在不同地雷密度情况下获胜的概率。三角形对应的曲线为初级 88，正方形为 1513，菱形为高级，3016 。这里的能否求解实际上不包括第一次随机点击的时候踩中雷的概率。[12]
我们把流体通过多孔介质逾渗的模型抽象出来的话，其实对应着点逾渗，也就是把整个介质想象成一个网络，流体在经过每个网格时，有概率 p 的可能通过。如果不能流过的网格在网络中连成了片，流体就不能流过了。
不严格地来说，求解扫雷问题其实和逾渗模型很类似，我们求解的过程其实也像推土机一样，不断地利用已有的知识将已知区域向外一层一层地推进。如果游戏中百思特网某处雷的密度越大，那么越有可能出现可解部分被雷分开的情况，地雷密度和逾渗参数起到了一样的作用。如果被分隔到无法连接整个棋盘，那就无法继续推理了。更为严格的证明可以参考 Elchanan Mossel 的论文。[13]

推土机，图片来自网络
随着网格的不断增大，这条胜率曲线中间部分也变得越来越陡峭，扫雷问题越来越向两个极端发展：要不就根本解不出来，要不就是很容易地就能解出来。在高级模式下，地雷的密度其实已经到了 99/480 = 0.2，能够解出来的概率已经不到 1/4，这还不算手抖了点错了，开局不好重开之类的情况，真的不算是友好了。
结论
Conclusion

emoji 版本扫雷 [14]
相信看到这里的人
一定已经跃跃欲试想要玩一下扫雷了
我相信你们
天下无难事，只要肯放弃
卸载也行