太极图探秘|最全最有价值的太极图多种描述( 四 )

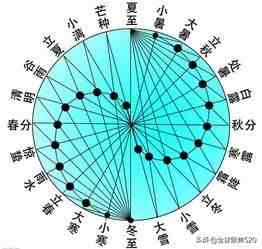
太极图数学模型
太极图数学模型在事物现象研究过程中的应用是相当普遍的，上面的质点匀速圆周运动系统就是其中的一例。下面就太极图数学模型的应用再举几个实例。
1. 月相现象
月相是指月球、地球和太阳三者在太空中相互运动形成的某一状态月光的反射现象。因为三者的相互运动都遵循着特定的规律，所以月相是周期性变化的，其周期取决于月球的公转周期、地球的自转和公转周期。经过长期的观察测定，月相周期为29.53天。月相按朔月、峨嵋月、上弦月、凸月、望月、凸月、下弦月、残月的过程在一个周期内循环一次。月相反映的是月球表面反射太阳光的面积大小，这可以用数学关系式表示。设月球的象视面积为S0，日照反光面方向与观察方向之间的角度用表示，当为0（反光面方向与观察方向相同）时月相为朔月，当为180度（反光面方向与观察方向相反）时月相为望月，当成90度直角时月相为上弦月或下弦月。那么，从朔月（初一）开始月球反光的明亮面积S+为
S+ = S0（1- cos) /2
不反光的阴暗面积S-为
S- = S0（1+ cos）/2
用明亮面积S+、阴暗面积S-函数在太极坐标系中绘制的图形如图四所示。

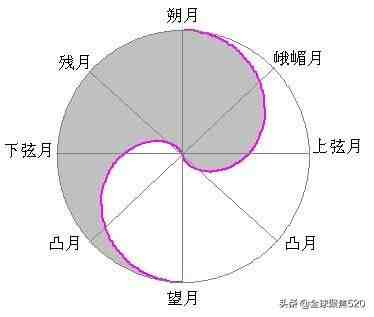
图1 月相阴阳太极图
该图旋转180度后与阴阳太极图完全吻合，月球的象视面积S0为太极系统的和H，明亮面积S+为太极系统的阳Y+，阴暗面积S-为太极系统的阴Y－。所以，月相告诉我们深藏于现象后面的阴极阳升、阳极阴返的变化规律，我们祖先的阴阳概念思维或许是从月相的观察中得到了启发。
2. 单摆运动
单摆是挂在一根细线下面的可以自由摆动的小球，如图五所示。许多著名的物理学家如伽利略、惠更斯、牛顿等等都对这一系统做过研究。

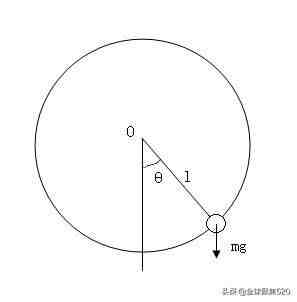
图2 单摆运动示意图
整个系统的全部质量可认为集中在可看做质点的小球上，为了使它能做任意大幅度的运动，可以把细线换成细棒。细棒的质量、空气的阻力相对较小可忽略。当拉开小球，使它偏离平衡位置，放手后小球受重力与拉力作用，沿着以平衡位置为中心的一段圆弧做往复运动，具有周期性变化规律。
设摆长为l，小球的质量为m相对于小球铅垂位置的角位移为，重力加速度为g，那么，单摆的重力势能为
Ep = mgl(1-cos)
单摆的动能为
Ek = mv2/2
由机械能守恒定律，单摆的总能量为
E＝Ek+ Ep＝mv2/2+ mgl(1-cos)＝常量
由于单摆系统除了受重力与拉力作用外不受其它因素影响，单摆的总能量由初始角位移0确定，当=0时单摆的动能为0，所以单摆的总能量为
E＝Ek+ Ep＝mgl(1-cos0)
单摆的单位总能量（无量纲）为
H≡E/ mgl＝(1-cos0)＝常量（5）
单摆的单位动能为
Hk = Ek / mgl＝H-(1-cos) （6）
单摆的单位重力势能为
Hp = Ep / mgl＝1-cos （7）
当0＝时，自由单摆的单位总能量为最大H=2，用单位动能Hk、单位重力势能Hp函数在太极坐标系上可绘制出单摆能量变化曲线，如图六所示。

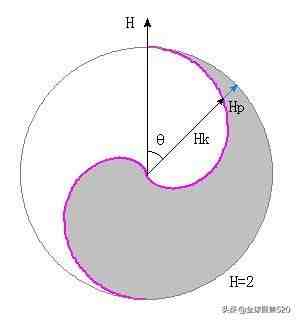
图3 单摆运动能量变化太极图
单摆运动能量变化太极图也是一个古太极图，只不过把太极系统百思特网的参数扩大了2倍，即单摆的单位总能量为太极系统的和的2倍，单位百思特网重力势能和单位动能也分别为太极阴、阳因子的2倍。
小球在重力作用下由静止状态（具有最大势能）开始摆动，运动产生了动能。随着小球位置的降低，势能渐渐减小，动能渐渐增加。等到小球经过最低位置时单摆能量全部转换为动能，之后，在惯性的作用下小球继续往高的位置运动，动能则慢慢地转换为势能。到达极高点时，小球因动能消失而趋向静止，静止所具有的是最大势能。在势能的作用下，静止之后的小球又向相反的方向恢复运动。单摆动能为阳，势能为阴，小球动静变化形成了单摆阴阳能量的变化，这正是《太极图说》所描述的“太极动而生阳，动极而静，静而生阴，静极复动”现象。
3. 康普顿效应
1922年，美国物理学家康普顿在研究石墨中的电子对X射线的散射时发现，有些散射波的波长比入射波的波长略大，这是光子和电子碰撞时，光子的一些能量转移给了电子。康普顿假设光子和电子、质子这样的实物粒子一样，不仅具有能量，也具有动量，碰撞过程中能量守恒，动量也守恒。按照这个思想列出方程后求出了散射前后的波长差，结果跟实验数据完全符合，这样就证实了他的假设。这种现象叫康普顿效应。