标准差和方差|一文了解无处不在的标准差( 二 )

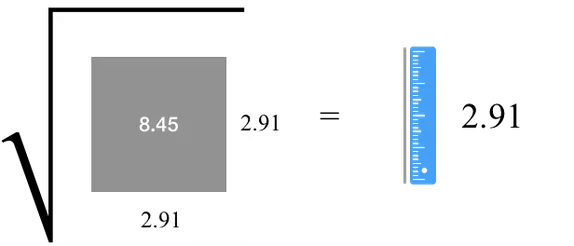
最后，我们终于得到了标准差：变异的平方根，即 2.91points 。
这就是标准差的核心理念。本文对标准差概念的基础直观解释可以帮助大家更容易地理解，为什么在处理 z 分数（z-score）、正态分布、标准误差和方差分析时要使用标准差的单位。
此外，如果你用标准差公式中的拟合线 Y 替代平均值，则你在处理的是基础回归项，如均方误差（不开根号的话）、均方根误差（开根号，但是和拟合线相关）。相关和回归公式均可使用不同量的平方和（或总变异区域）来写。分割平方和是理解机器学习中的泛化线性模型和偏差-方差权衡的关键概念。
简而言之：标准差无处不在。
绝对值的问题
你可能会疑惑，为什么对差异求平方而不是取绝对值呢。没有什么能够真正阻止你使用差异的平均绝对值。平均绝对值给所有差异提供的是相同的权重，而差异平方为距离平均值较远的数字提供更多权重。这或许是你想要的。但是，大部分数学理论利用差异平方（其原因不在本文讨论范围内，如可微分）。
不过，我会用一个容易理解的反例来回答这个问题。假设有两个均值相同的分数集合：x_1 和 x_2：

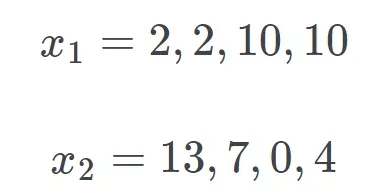
从这些数字中，你可以轻松观察到 x_1 的变异和数值分散性比 x_2 低。我们来计算两个集合差异的平均绝对值（二者的平均值都为 6）：

哦，结果并不好！两个集合的变异值相同，尽管我们能够看到 x_1 的数字差异要比 x_2 低。现在，我们使用差异平方计算，得到：

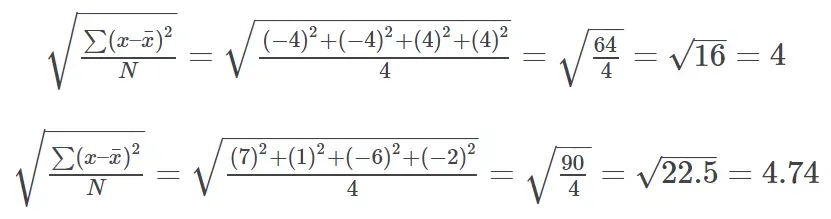
在差异平方的作用下，我们得到了想要的结果：当数字越分散时，标准差越大。

标准差和方差|一文了解无处不在的标准差( 二 )

【标准差和方差|一文了解无处不在的标准差】