什么是合数|认识质数和合数

什么是合数（认识质数和合数）
今天给大家讲一讲有关质数与合数的一些简单知识和小故事。

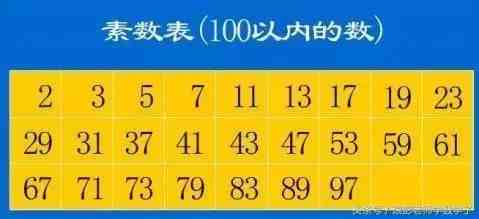
概念质数：
质数（prime number）又称素数，在自然数中除了1和它本身以外不再有其他因数，如3,7,19,23等。质数有无限个。合数：（Composite number），是指在自然数中除了1和它本身之外还有别的因数，这样的数叫做合数。如4 ， 6 ， 9 ， 15 ， 49等都是合数。
皮耶德费马（Pierre de Fermat）是一个17世纪的法国律师，也是一位业余数学家。之所以称业余，是由于皮耶德费马具有律师的全职工作。根据法文实际发音并参考英文发音，他的姓氏也常译为“费尔玛”（注意“玛”字）。费马最后定理在中国习惯称为费马大定理，西方数学界原名“最后”的意思是：其它猜想都证实了，这是最后一个。著名的数学史学家贝尔（E. T. Bell）在20世纪初所撰写的著作中，称皮耶德费马为”业余数学家之王“ 。
贝尔深信，费马比皮耶德费马同时代的大多数专业数学家更有成就。17世纪是杰出数学家活跃的世纪，而贝尔认为费马是17世纪数学家中最多产的明星历史故事：费马数2^(2^n)+1 被称为“17世纪最伟大的法国数学家百思特网”的费马，也研究过质数的性质。他发现，设F(n)=2^(2^n)+1 ，则当n分别等于0、1、2、3、4时， Fn分别给出3、5、17、257、65537 ，都是质数，由于F5太大（F5=4294967297），他没有再往下检测就直接猜测：对于一切自然数， Fn都是质数。这便是费马数。但是，就是在F5上出了问题！费马死后67年， 25岁的瑞士数学家欧拉证明：F5=4294967297=6416700417 ，它并非质数，而是一个合数！更加有趣的是，以后的Fn值，数学家再也没有找到哪个Fn值是质数，全部都是合数。目前由于平方开得较大，因而能够证明的也很少。现在数学家们取得Fn的最大值为：n=14百思特网95 。这可是个超级天文数字，其位数多达10^10584位，当然它尽管非常之大，但也不是个质数。质数和费马开了个大玩笑！这又是一个合情推理失败的案例！马林梅森（Marin Mersenne,1588.9.8–1648.9.1）是17世纪法国著名的数学家和修道士，也是当时欧洲科学界一位独特的中心人物， 1588年9月8日生于曼恩省的瓦兹， 1648年9月1日卒于巴黎。他与大科学家伽利略、笛卡尔、费马、帕斯卡、罗伯瓦、迈多治等是密友梅森素数
17世纪还有位法国数学家叫梅森，他曾经做过一个猜想：2^p-1 ，当p是质数时， 2^p-1是质数。他验算出了：当p=2、3、5、7、17、19时，所得代数式的值都是质数，后来，欧拉证明p=31时， 2^p-1是质数。p=2 ， 3 ， 5 ， 7时， 2^p-1都是素数，但p=11时，所得2047=2389却不是素数。还剩下p=67、127、257三个百思特网梅森数，由于太大，长期没有人去验证。梅森去世250年后，美国数学家科勒证明， 2^67-1=193707721761838257287 ，是一个合数。这是第九个梅森数。20世纪，人们先后证明：第10个梅森数是质数，第11个梅森数是合数。质数排列得这样杂乱无章，也给人们寻找质数规律造成了困难。现在，数学家找到的最大的梅森数是一个有9808357位的数：2^32582657-1 。数学家虽然可以找到很大的质数，但质数的规律还是无法循通
经典试题质数、合数练习题
1. 下面的数中，哪些是合数，哪些是质数。1、13、24、29、41、57、63、79、87 合数有：质数有：2. 写出两个都是质数的连续自然数。（）3. 写出两个既是奇数，又是合数的数。（）4. 判断：（1）任何一个自然数，不是质数就是合数。（）（2）偶数都是合数，奇数都是质数。（）
（3）7的倍数都是合数。（）
（4）20以内最大的质数乘以10以内最大的奇数，积是171 。（）
（5）只有两个约数的数，一定是质数。（）