什么是素数|素数的魅力( 二 )

高斯发现，随着数值增大，素数出现的频率会逐渐降低，遵循“反对数”定律。虽然高斯的素数分布定理并没有算出素数数目的精确值，但他给出了一个非常好的近似值。例如，根据素数定理预测在 1000000 到 1001000 之间存在 72 个素数，而正确结果是 75，误差在 4% 左右。这令他提出一个猜想：，其中为不大于 x 的素数个数。也就说当 x 趋近无限时，有下式成立：
而在这个猜想提出一个世纪之后，这个称之为素数定理(prime number theorem)才得到了证明。

(x), x/lnx 和 (x)/(x/lnx) 的比较
随着素数计数范围越来越大，估计值与真实值的相对误差将趋近于 0 。悬赏百万奖金，位列当今数学界七大难题之一的黎曼猜想(Riemann hypothesis)，也描述了高斯定理估算的精确程度。
素数定理和黎曼猜想已经得到了人们的广泛关注，但它们在早期，都是从枯燥的素数表数据分析开始的。现在，我们获取数据的方式都来自于计算机程序的运算，不再需要手算筛选，但数学家们仍在寻找素数研究的新模式。除了 2 和 5 之外，所有素数都以 1，3，7 或 9 结尾。19 世纪，人们发现这几个末位数字在素数中存在相同的出现频率。换句话说，如果你计数到 100 万，25%的素数末位为 1，2百思特网5% 末位为 3，25% 末位为 7，25% 末位为 9 。

对素数末位数字的分析除了 2 和 5 之外，所有素数都以 1，3，7 或 9 结尾。19 世纪，人们发现这几个末位数字在素数中存在相同的出现频率。

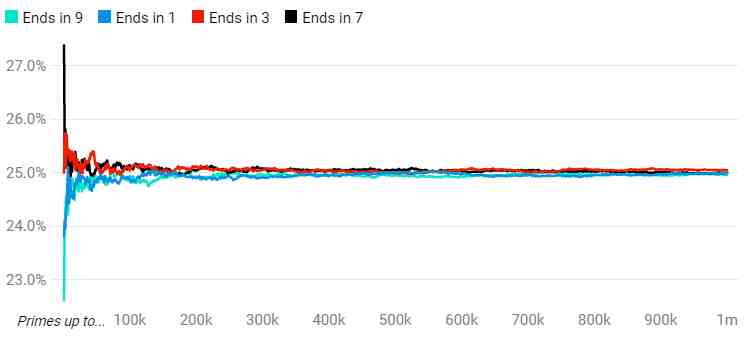
?图表来自：The Conversation, CC-BY-ND，作者Martin Weissman
几年前，斯坦福大学的数论学家莱姆克奥利弗(Lemke Oliver) 和坎南桑德拉贾恩(Kannan Soundararajan)在实验中观察素数及其下一个相邻素数的末位数字规律，意外发现了一个问题。例如，23 之后的素数是 29，它们的末位数字是前 3 后 9 。那么，相邻两个素数的末位数字，是前 3 后 9 常见，还是前 3 后 7 常见呢?

100 万以内的连续素数末位数字对出现的频率。相同颜色代表末位数字对具有相同的间距值。(M.H. Weissman, CC BY)
数论学家们预计会存在一些差异，但实验结果远超预期。将相邻素数末位数字对按照间距不同进行分组，譬如，23 与 29 间距为 6 。结果发现，像 23 和 29 这样前 3 后 9 的素数对儿的占比，超过先 7 后 3 的素数对儿占比，尽管两种情况中相邻素数对儿的间距都为 6 。虽然数学家们很快给出了一种较为可信的解释。但是，当涉及到连续素数的研究时，数学家们大部分还局限在分析数据进而寻找合理解释的阶段，距离揭示真相的唯一标准——数学上证明，似乎还需要很长一段路要走。