有理数和无理数|从有理数与无理数的比较开始( 二 )
补充一下可数集概念:能与百思特网自然数集建立一一对应关系百思特网的集合 。
可数集的基数是最小的无穷量,康托尔把这个量记为?0(希伯来文,读作“阿列夫零”) 。同时康托尔指出,阿列夫零是最小的无穷量,那比阿列夫零更大的无穷在哪呢?
NO.4上场吧!无理数
无理数可数吗?或者说实数可数吗?
答案是:NO
康托尔运用对角线法来论证这一点,证明过程很短,却堪称精妙绝伦!(妈妈问我为何跪下看书系列)
考虑整个实数集是否可数,我们先考虑0-1之间的所有实数是否可数 。假设存在某种规则能够列出0-1之间的所有实数:
0.1598545445……
0.6589745454……
0.5968974132……
0.9887946456……
0.3521587487……
0.1659842412……
……
以上的数随便写的,此时康托尔问,0.267865……在什么位置?
这个数是怎么取的呢?取第一个数的第一位小数加1,取第二个数的第二位小数加1,取第三个数的第三位小数加1,取第四个数的第四位小数加1……,也就是上面数中红色的数字加1 。
假如0.267865……在第n个位置上,则它的第n位小数应该等于第n个数(也就是它自身)的第n位小数加1 。
简单说,这个数的第n位小数等于它本身第n位小数加1 。显然这是不可能存在的!

所以不存在任何一种方法能够把0-1之间所有的实数全部列举出来,当然也不可能存在一种方法能够把全体实力列出来 。
像这样的无穷称为不可数无穷,不管你承认还是不承认,同样是无穷,也能分出不同种类 。无理数集、实数集称为不可数集 。
在数轴上任取一段线段,由这些连续着的点构成的集合均为不可数集,又称连续统 。基数记为c 。
NO.5 c=?1
既然已经明确了有理数代表着可数无穷,而无理数则代表着不可数无穷,那可数与不可数到底谁更多呢?换句话说,?0与c谁更大呢?
事实上,从概率的角度来看,在数轴上任取一点,取到有理数的概率为0 。
无理数是无限不循环小数,有理数包含整数、有限小数和无限循环小数,我们可以把整数和有限小数看成后面的小数位均为0的数,举个例子,1.8=1.800000……,后面的小数位都是0 。
现在我们给一个数填充小数位,有无数个小数位需要我们填充,而填充的数字都是随机取的,所以说都取0或者说取到一列循环数的概率为0 。借助于这样一个想法,无理数不仅比有理数多,而且多得多!
怎么样能够比无穷还要多?
对于集合{1},它有两个子集:空集、{1},子集组成的集合的基数为2^1;对于集合{1,2},它有四个子集空集、{1}、{2}、{1,2},子集组成的集合的基数为2^2,以此类推,若一个集合的基础为n,则其子集构成的幂集基数是2^n 。
那如果原集合的基数是?0呢?
事实上,康托尔已经证明出,c=2^?0,这里的?0是无穷大的,所以能想象c有多大吗?

康托尔所做的事情不止于此,他还猜想,在?0和c之间不存在其他的无穷,即在?0后的下一个无穷量便是c,即c=?1(?1即?0后一个无穷量),这就是著名的“连续统假说” 。1900年世界数学家大会上,希尔伯特把这个问题排在了20世纪23大有待解决的重要数学问题之首 。
NO.6 数轴上见分晓!
关于数轴,我们都知道数轴上的点与实数是一一对应的,或许会存在这样的想法,任意两个有理数之间还存在无数个有理数,此外有理数与有理数之间还会有缝隙,那便是无理数,这个缝隙有多少并不为我们所知,但两有理数之间还存在着无数个有理数是必然的 。
所以有人会说有理数像砖,构成了数轴的主体,无理数像是胶水,把砖与砖之间的缝隙补充完整,构成一条完整的数轴 。
从两者的数量对比来看,显然以上的想法大错特错,无理数更像是构成数轴的砖,占据着数轴的绝大部分 。说来说去其实就是这么一个问题:有理数和无理数在数轴上是如何分布的?
借用一下狄利克雷函数:
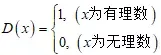
这就是把有理数与无理数作个分离,那函数图像长啥样?也许是这样?
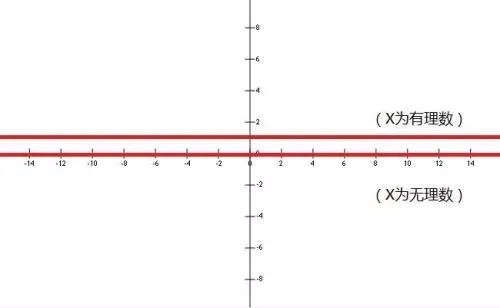
- 私人影院|私人影院和电影院能同步上映吗
- 春天|2022春天什么时候开始暖和
- 《浮生六记》:和相处舒服的人在一起,才是最好的养生
- 生根粉|生根粉和多菌灵可以一起浇花吗
- 认真和你交往的男人,其实是有迹可循的
- 植物|植物补光灯和普通照明灯有什么区别
- 面霜|面霜品牌排行榜前十名,面霜品牌排行榜
- 地震|猫能感知地震吗
- 呼和浩特|2020呼和浩特各区县人口排行 呼和浩特历年常住人口数
- 冰墩墩|冰墩墩和雪容融哪个贵
