人脸检测综述|人脸检测和识别技术的文献综述( 三 )
3.2.3 基于统计的方法
统计方法是目前最受注意的一类方法 。它的思想就是想通过学习来得
到人脸的统计特征,并以此来判别分类 。其学习和识别过程的模型如下图
4所示 。
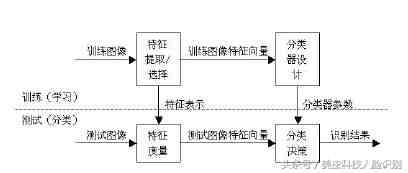
图4 统计方法识别模型
子空间分析(Subspace Analysis)方法是其中的主要的一种,它的思想就是把高维空间中松散分布的人脸图像,通过线性或非线性变换压缩到一个低维的子空间中去,在低维的子空间中使人脸图像的分布更紧凑,更有利于分类 。另外,也使高维的计算减小为低维计算 。目前在人脸识别中得到成功应用的线性子空间分析方法有:主元分析(Principal ComponentAnalysis / PCA)、线性判决分析(Linear Discriminant Analysis / LDA)、独立元 分 析 (Independent Component Analysis / ICA) 、 非 负 矩 阵 因 子(Non-negative Matrix Factorization / NMF);基于核技巧的非线性子空间分析有:核主元分析(Kernel Principal Component Analysis / KPCA)和核 Fisher判决分析(Kernel Fisher Discriminant Analy百思特网sis / KFDA) 。
核主元分析法如下:
基于线性子空间分析方法的人脸识别,实际上是把实际人脸图像中存
在的表情、姿态、光照等复杂的变化进行了线性简化,因此不可能得到充分的描述 。核技术的思想就是利用一非线性映射,把原空间的数据映射到一隐特征空间 F 中::x ∈Rn →f∈F,然后在隐特征空间中对数据进行分析,从而可得到有效地分析原始数据的非线性关系 。而在计算上,并不需要明确的计算这个非线性变换,只需要计算在隐特征空间 F 中两两向量的点积即可(3.1) 。隐特征空间 F 就是通过这样的点积来描述的 。
k ( x,y)= ((x)*(y)) (3.1)
常用的点积核函数有三种:多项式点积核函数、径向基点积核函数和
Sigmoid 点积核函数[14-16] 。
核主元分析是由 Scholkopf 等[17]首先提出来的,其思想就是把核技术
和主元分析结合起来 。首先用核技术把原始数据投影到隐特征空间 F 中,
再对其作线性主元分析,那么就得到了相对于原空间的一个非线性主元子
空间 。根据主元分析的原理,求解在隐特征空间 F 中的主元就等同于求解
如下的特征值问题:
w=Sw (3.2)
其中,S表示样本在隐特征空间 F 中投影的离散度矩阵 。
因为在隐特征空间中作线性变换,所以存在这样的关系:对应于 ≠0
的特征向量 w 必存在于由(x1),(x2),...,(xN)所张成的空间中 。数学
上就可把 w用式(3.3)来表示:
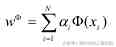
(3.3)
把(3.3)代入(3.2)中,则特征值的求解问题就变
成了解下面的特征值问题:
N =K (3.4)
其中,矩阵 K 是一个 N × N的矩阵,Ki,j= k(xi,xj)=((xi),(xj)),
=(1 ,2,...,N )T 。
同理,可以选择对于前 m 个大的特征值的特征向量作为隐特征空间 F
中的主元,那么原空间中数据 x 在 w上的投影就是:
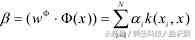
(3.5)
4、小结与展望
随着社会的不断发展,传统的身份识别技术已经不能满足人们的需要 。与其它生物特征识别技术相比,人脸识别在可用性方面具有独到的技术优势,这主要体现在:可以隐蔽操作,尤其适用于安全监控;非接触式采集,没有侵犯性,容易被接受,不会对用户造成生理上的伤害,容易被大多数的用户接受;具有方便、快捷、强大的事后追踪能力;图像采集设备成本低;更符合人类的识别习惯,可交互性强[18] 。
人脸检测是人脸信息处理领域的一个重要课题,也是计算机视觉和人机交互领域中的研究热点 。这一问题的突破性进展将给人脸识别、表情姿态的识别、视频监控、身份验证等相关领域的研究带来很大的推动作用[19] 。人脸检测和识别是极具挑战性的研究课题,需要进一步研究和解决的问题还有很多 。人脸检测和识别的难度大,人脸识别技术经过几十年的研究,在环境可控的条件下已经达到了实用程度,但是在考虑光照,姿态,表情等变化的影响时,其应用范围受到了较大的限制 。
近年来,为了进一步解决人脸识别的表情,姿态等问题,三维人脸识别技术得到了较大的发展,三维人脸模型重建方法也日趋增多 。但是如何将三维识别的结果融合到二维识别中,从而建立一个有效识别准则,还有待进一步讨论,人脸特征的选取与提取算法等方面还需要进一步优化[20] 。
【人脸检测综述|人脸检测和识别技术的文献综述】
- 核酸检测|48小时核酸检测到另一个地方过了怎么办
- 核酸检测|48小时核酸检测报告可以别人代领吗
- 核酸检测|48小时核酸检测29号做核酸到31号能用吗
- 核酸检测|48小时核酸检测晚上可以做吗
- 核酸检测|绿码带星号做了核酸可以吗
- 核酸检测|48小时核酸检测全国通用吗
- 核酸检测|48小时核酸检测多久出结果
- 坐车|坐车超过48小时核酸检测怎么办
- 春节|2022年春节回衡水需要核酸检测吗
- 农产品检测委托书范文有没有?
