初等函数|基本初等函数的图像与性质
初等函数(基本初等函数的图像与性质)
在数学的发展过程中,形成了最简单最常用的六类函数,即常数函数、幂函数、指数函数、对数函数、三角函数与反三角函数,这六类函数称为基本初等函数 。
一、常数函数
y = c 或 f ( x ) = c , x ∈ R ,其中 c 是常数 。它的图像是通过点 (0,c),且平行 x 轴的直线,如下图所示:
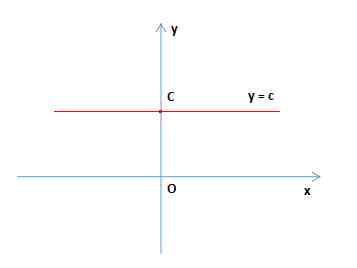
常数函数的图像
常数函数的性质:
1、常数函数是百思特网有界函数,周期函数(没有最小的正周期)、偶函数;
2、常数函数既是单调增加函数又是单调减少函数,特别的当 c = 0 时,它还是奇函数。
二、幂函数
1、形如 y = x^a 的函数是幂函数,其中 a 是实数。

幂函数图(1)
2、常见幂函数的图像:
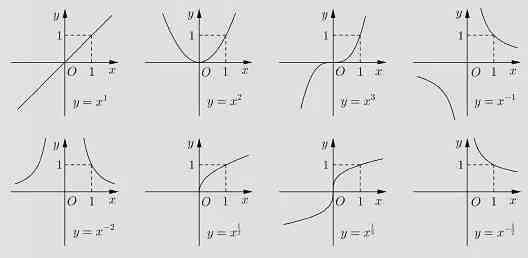
幂函数图(2)
注:画幂函数图像时,先画第一象限的部分,在根据函数奇偶性完成整个图像 。
3、幂函数的性质:
① 幂函数的图像最多只能同时出现在两个象限,且不经过第四象限;如图与坐标轴相交,则交点一定是坐标原点。
② 所有幂函数在 (0,+∞)上都有定义,并且图像都经过点 (1,1) 。
③ 若 a > 0 , 幂函数图像都经过点 (0,0)和(1,1),在第一象限内递增;
若 a < 0,幂函数图像只经过点 (1,1),在第一象限内递减。
三、指数函数
1、一般地,函数 y = a^x (a > 0 且 a ≠ 1)叫做指数函数,自变量 x 叫做指数,a 叫做底数,函数的定义域是 R 。
2、指数函数的图像:
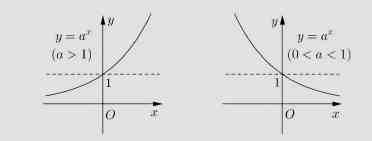
指数函数图象
3、指数函数的性质:
① 指数函数 y = a^x (a > 0 且 a ≠ 1)的函数值恒大于零,定义域为 R,值域为 (0,+∞);
② 指数函数 y = a^x (a > 0 且 a ≠ 1)的图像经过点 (0,1);
③ 指数函数 y = a^x (a > 1)在 R 百思特网上递增,指数函数 y = a^x (0 < a < 1)在 R 上递减。
四、对数函数
1、对数及其运算:
一般地,如果 a (a > 0 , a ≠ 1)的 b 次幂等于 N,即 a^b = N,那么 b 叫做以 a 为底 N 的对数;
记作:logaN = b , 其中 a 叫做对数的底数,N 叫做真数 。
根据对数定义可知:
① 零和负数没有对数,真数大于零;② 1 的对数为 0,即 loga1 = 0 ;
③ 底的对数等于 1,即 logaa = 1 ;④ 对数恒等式:a^(logaN) = N 成立。
通常以 10 为底的对数叫做常用对数,常用对数 log10N 简记作 lgN;
以无理数 e = 2.71828 ... 为底的对数叫做自然对数,自然对数 logeN 简记作 lnN。
对数运算性质:如果 a > 0 , a ≠ 1 , M > 0 , N > 0 , 那么 :
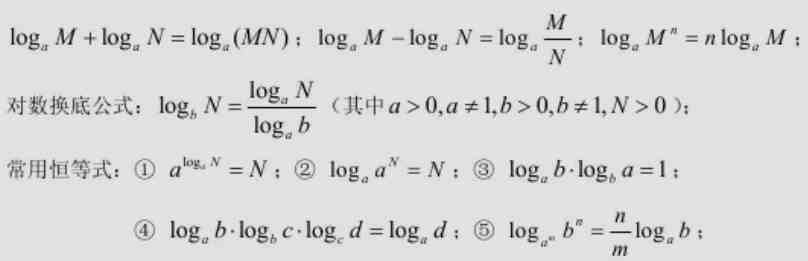
对数运算性质图
2、对数函数:
一般地,对数函数 y = logax (a > 0 且 a ≠ 1)就是指数函数 y = a^x (a > 0 且 a ≠ 1)的反函数 。
因为指数函数 y = a^x (a > 0 且 a ≠ 1)的值域是 (0,+∞),
所以对数函数 y = logax (a > 0 且 a ≠ 1)的定义域是 (0,+∞) 。
3、对数函数的图像:
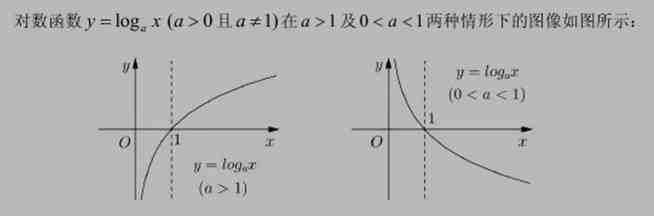
对数函数的图像
4、对数函数 y = logax (a > 0 且 a ≠ 1)的性质:
① 对数函数 y = logax (a > 0 且 a ≠ 1)的图像都在 y 轴的右侧,定义域是 (0,+∞),值域是 R ;
② 对数函数 y = logax (a > 0 且 a ≠ 1)的图像都经过点 (1,0);
③ 对数函数 y = logax (a > 1): 当 x > 1 时,y > 0 ;当 0 < x < 1 时,y < 0 ;
对数函数 y = logax&百思特网nbsp;(0 < a < 1): 当 x > 1 时,y < 0 ;当 0 < x < 1 时,y > 0。
④ 对数函数 y = logax (a > 1)在 (0.+∞)上是增函数,
对数函数 y = logax (0 < a < 1)在 (0.+∞)上是减函数 。
五、三角函数与反三角函数
1、三角函数:y = sin x , y = cos x , y = tan x , y = cot x ;
2、反三角函数 : y = arcsin x , y = arccos x , y = arctan x , y = arccot x。
3、三角函数的图像:
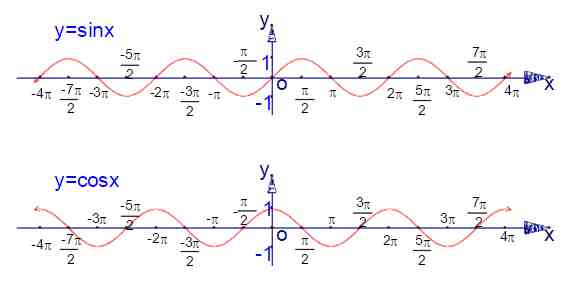
三角函数图像(1)
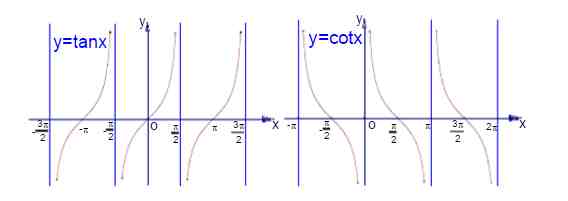
- 公寓|公寓个人可以买卖吗
- 三维空间基本原理读后感锦集
- 最新电子商务简历怎么写?
- 工商管理大学生简历写法怎么样?
- 拜访基本礼仪知识怎么写?
- 计算机专业学生简历如何写?
- 年计算机专业学生简历怎么写?
- 年护理学专业简历如何写?
- 房子|房子查封多久强制执行
- 前台接待员的求职简历怎么写?
