噪声预测|噪声预测的无监督学习( 二 )

之间的“均方距离”达到最小值。一旦配对成功，已配对的表征和噪声向量之间的“均方距离”就能被视为测量分布均匀性的度量单位。确实，这是对“瓦瑟斯坦距离”（Pz分布和均匀分布之间的距离）的一种经验性估测。

信息最大化的表征就一定是好的表征吗？过去的几天，我做了太多这种类型的讲话——什么是一个好的表征？无监督的表征学习究竟是什么意思？对于InfoMax表征，你同样可以提出这样的问题：这是找到一个好表征的最佳指导原则吗？
还不够。对于新手，你可以以任意的方式转换你的表征，只要你的转换是可逆的，百思特网那么“互信息”就应该是相同的。所以你可以在可逆的条件下对你的表征做任何转换，无需考虑InfoMax的目标。因此，InfoMax标准不能单独找到你转换过的表征。
更有可能出现的是，我们在操作经验中所看到的那些成功案例都是ConvNets与InfoMax原则联合使用的结果。我们仅在ConvNet比较容易展示的表征中，对信息进行最大化操作。

本文总结NAT的表征学习原则可以理解为寻找InfoMax表征，即最大化地保留了输入数据的信息的有限熵的表征。在“卷积神经网络范例”中也存在类似的信息最大化的解读，它根据数据点的噪声版本来估测这个数百思特网据点的指数。在开始的时候，你肯定会认为这些算法很奇怪，甚至是超乎常理的，但是如果我们把这些算法重新理解为信息最大化工具，我们就会对他们有所改观。反正至少我对他们是有了更深的认识和理解的。

特别内容：一些关于EMD随机版本的小提示以这种文字的方式实施EMD度量的难处在于，你需要找到一个最优的分配方案，分配好两个实操经验上的分布和尺度
。那么为了回避这个难题，作者提出了一个“最优分配矩阵”的任意更新升级，即所有的配对一次只进行一小批更新升级。
我并不指望这个“最优分配矩阵”能有多有用，但是值得一提的是，这一矩阵使这个算法很容易陷入局部的最小值。假设表征
的参数是固定的，我们变化、更新的只是其中的分配。我们来看下面图形中的解读：

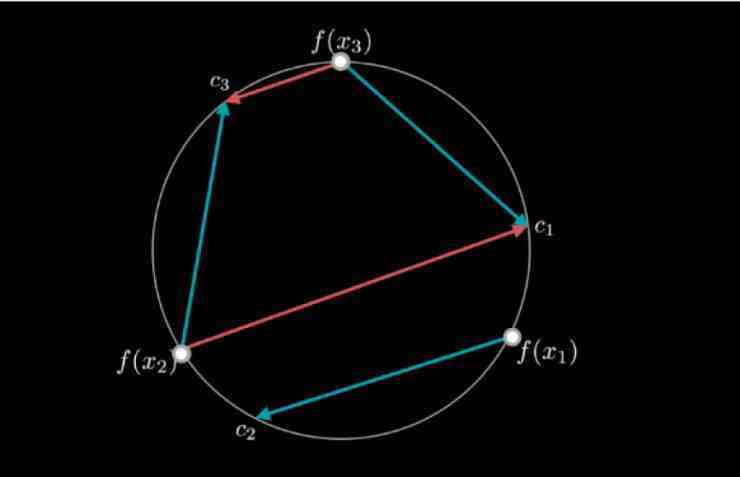
在这个2D的球状单位（圆圈）上的X1，X2，X3分别是三个数据点，这些数据点之间距离相等。是三个可能的噪声分配，三者之间也是距离相等。C1,C2,C3很明显，其中的最优分配就是把X1与C1配对，X2与C2配对，X3与C3配对。
假设，我们当前的映射是次优的，如图中蓝色箭头指示的；而且我们现在只能在尺寸2的minibatch上更新分配。在尺寸2的minibatch上，我们的分配只有两种可能性：第一，保持原来的分配不变；第二，把所有的点都互换，就像图中红色箭头指示的。在上图这个例子中，保持原来的分配（蓝色箭头）比互换所有的点（红色箭头）更可行。因此，minibatch的更新将会使minibatch算法陷入这个局部的最小值。
但是这并不意味着这个方法没有用。当
也同时被更新了的情况下，这个方法确实能让算法摆脱这个局部最小值。其次，batch的尺寸越大，就约难找到这样的局部最小值，那么算法也就越不会陷入最小值。
我们可以转换一种思维方式，把这个任意的“匈牙利算法”的局部最小值看作是一个图表。每一个节点代表一个分配矩阵状态（一个分配排列），每一条边对应一个基于minibatch的有效更新。一个局部最小值就是一个节点，这个最小值节点与其周边的N!节点相比成本较低。
如果我们把原本大小为B的minibatch扩大到一个总样本的尺寸N，那么我们就会在图中得到一个N!节点，而每个节点百思特网都会超出额度，达到
。那么任意两个节点连接的概率就是
。Batch的B尺寸越大，我们这个图表就会变得越紧密，局部最小值也就不存在了。