递归算法流程图|递归详解( 二 )

int factorial (int n){ if(n==1){ return 1; } return n * factorial(n-1);}「注意啦」，不是所有递推函数的等价关系都像阶乘这么简单，一下子就能推导出来。需要我们多接触，多积累，多思考，多练习递归题目滴~
leetcode案例分析来分析一道leetcode递归的经典题目吧~

?
原题链接在这里哈：https://leetcode-cn.com/problems/invert-binary-tree/
?

「题目：」翻转一棵二叉树。
输入：
     4   /   \  2     7 / \   / \1   3 6   9输出：
     4   /   \  7     2 / \   / \9   6 3   1我们按照以上递归解题的三板斧来：
「1. 定义函数功能」
函数功能（即这个递归原问题是），给出一颗树，然后翻转它，所以，函数可以定义为：
//翻转一颗二叉树public TreeNode invertTree(TreeNode root) {}/** * Definition for a binary tree node. * public class TreeNode { *     int val; *     TreeNode left; *     TreeNode right; *     TreeNode(int x) { val = x; } * } */「2.寻找递归终止条件」
这棵树什么时候不用翻转呢？当然是当前节点为null或者当前节点为叶子节点的时候啦。因此，加上终止条件就是：
//翻转一颗二叉树public TreeNode invertTree(TreeNode root) {    if(root==null || (root.left ==null && root.right ==null)){       return root;    }}「3. 递推函数的等价关系式」
原问题之你要翻转一颗树，是不是可以拆分为子问题，分别翻转它的左子树和右子树？子问题之翻转它的左子树，是不是又可以拆分为，翻转它左子树的左子树以及它左子树的右子树？然后一直翻转到叶子节点为止。嗯，看图理解一下咯~

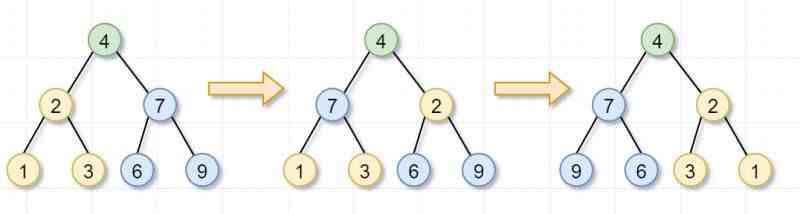
首先，你要翻转根节点为4的树，就需要「翻转它的左子树（根节点为2）和右子树(根节点为7）」。这就是递归的「递」的过程啦

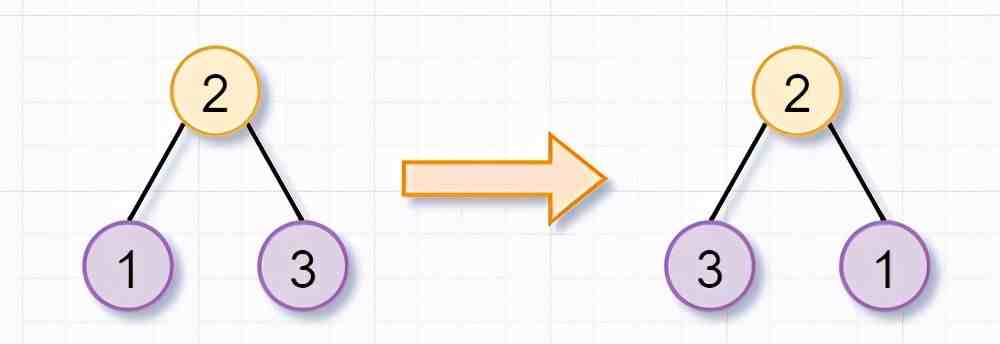
然后呢，根节点为2的树，不是叶子节点，你需要继续「翻转它的左子树（根节点为1）和右子树（根节点为3）」。因为节点1和3都是「叶子节点」了，所以就返回啦。这也是递归的「递」的过程~

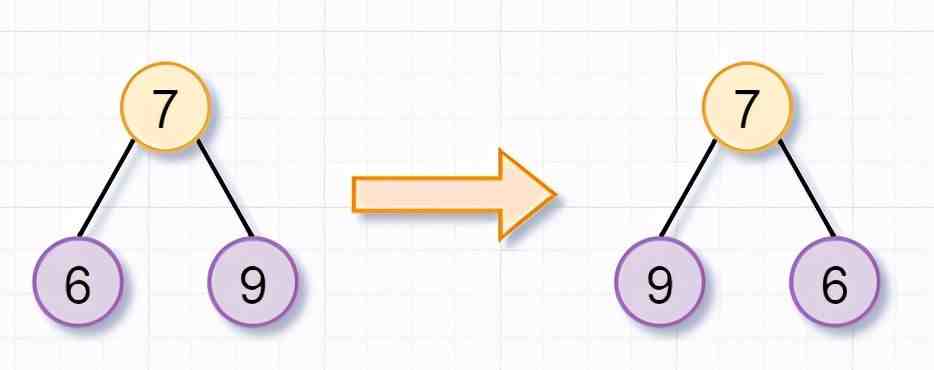
同理，根节点为7的树，也不是叶子节点，你需要翻转「它的左子树（根节点为6）和右子树（根节点为9）」。因为节点6和9都是叶子节点了，所以也返回啦。

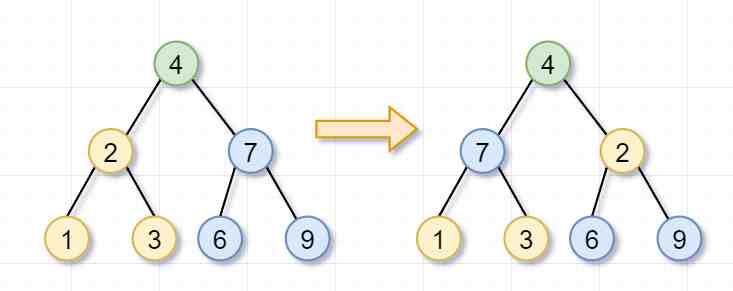
左子树（根节点为2）和右子树(根节点为7）都被翻转完后，这几个步骤就「归来」，即递归的归过程，翻转树的任务就完成了~

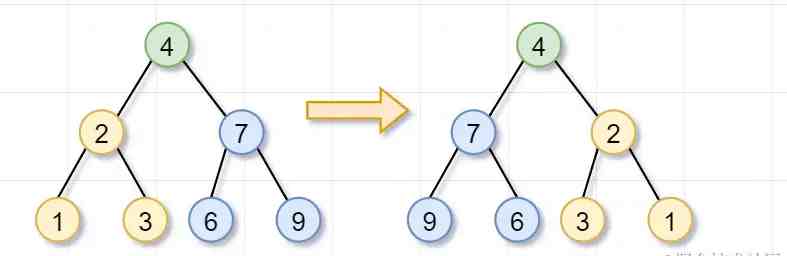
显然，「递推关系式」就是：
invertTree（root）= invertTree（root.left） + invertTree（root.right）;于是，很容易可以得出以下代码：
//翻转一颗二叉树public TreeNode invertTree(TreeNode root) { if(root==null || (root.left ==null && root.right ==null){ return root; } //翻转左子树 TreeNode left = invertTree(root.left); //翻转右子树 TreeNode right= invertTree(root.right);}这里代码有个地方需要注意，翻转完一棵树的左右子树，还要交换它左右子树的引用位置。
root.left = right; root.right = left;因此，leetcode这个递归经典题目的「终极解决代码」如下：
class Solution { public TreeNode invertTree(TreeNode root) { if(root==null || (root.left ==null && root.right ==null)){ return root; } //翻转左子树 TreeNode left = invertTree(root.left); //翻转右子树 TreeNode right= invertTree(root.right); //左右子树交换位置~ root.left = right; root.right = left; return root; }}