递归算法流程图|递归详解( 三 )

拿终极解决代码去leetcode提交一下，通过啦~

递归存在的问题递归调用层级太多，导致栈溢出问题
递归重复计算，导致效率低下
栈溢出问题每一次函数调用在内存栈中分配空间，而每个进程的栈容量是有限的。
当递归调用的层级太多时，就会超出栈的容量，从而导致调用栈溢出。
其实，我们在前面小节也讨论了，递归过程类似于出栈入栈，如果递归次数过多，栈的深度就需要越深，最后栈容量真的不够咯
「代码例子如下：」
/** * 递归栈溢出测试 */public class RecursionTest { public static void main(String[] args) { sum(50000); } private static int sum(int n) { if (n <= 1) { return 1; } return sum(n - 1) + n; }}「运行结果:」
Exception in thread "main" java.lang.StackOverflowError at recursion.RecursionTest.sum(RecursionTest.java:13)怎么解决这个栈溢出问题？首先需要「优化一下你的递归」，真的需要递归调用这么多次嘛？如果真的需要，先稍微「调大JVM的栈空间内存」，如果还是不行，那就需要弃用递归，「优化为其他方案」咯~
重复计算，导致程序效率低下我们再来看一道经典的青蛙跳阶问题：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
绝大多数读者朋友，很容易就想到以下递归代码去解决：
class Solution { public int numWays(int n) { if (n == 0){ return 1; } if(n <= 2){ return n; } return numWays(n-1) + numWays(n-2); }}但是呢，去leetcode提交一下，就有问题啦，超出时间限制了

为什么超时了呢？递归耗时在哪里呢？先画出「递归树」看看：

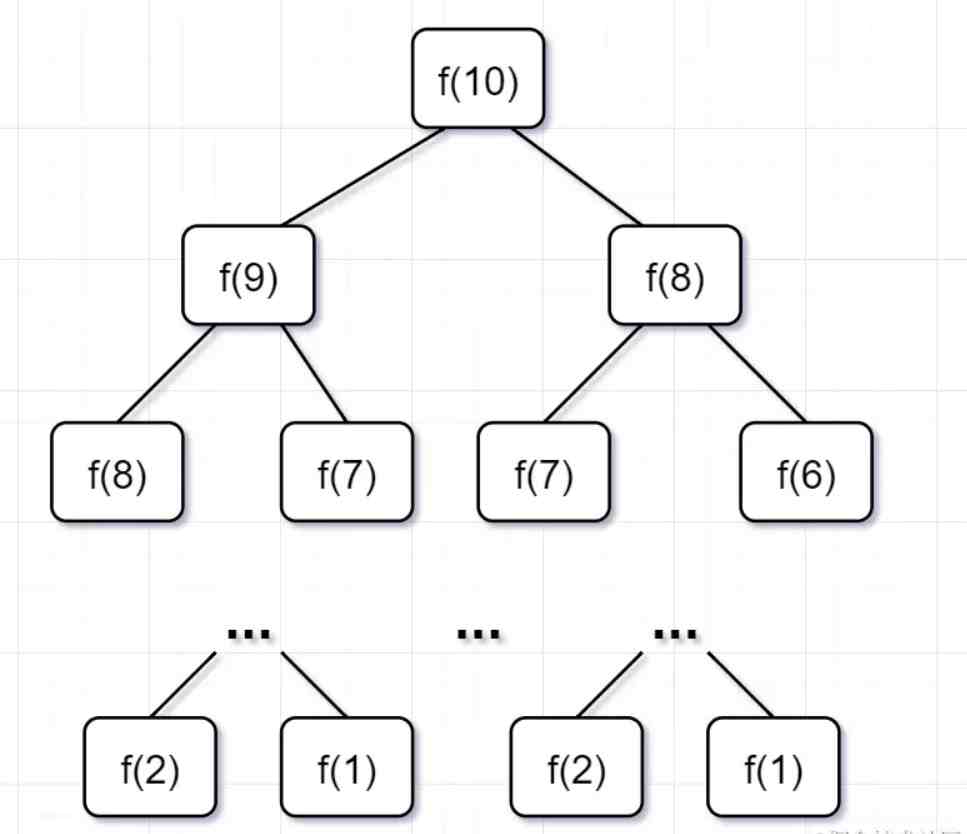
要计算原问题 f(10)，就需要先计算出子问题 f(9) 和 f(8)
然后要计算 f(9)，又要先算出子问题 f(8) 和 f(7)，以此类推。
一直到 f(2) 和 f(1），递归树才终止。
我们先来看看这个递归的时间复杂度吧，「递归时间复杂度 = 解决一个子问题时间*子问题个数」
一个子问题时间 = f（n-1）+f（n-2），也就是一个加法的操作，所以复杂度是「O(1)」；
问题个数 = 递归树节点的总数，递归树的总结点 = 2^n-1，所以是复杂度「O(2^n)」。
因此，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n)，就是指数级别的，爆炸增长的，「如果n比较大的话，超时很正常的了」。
回过头来，你仔细观察这颗递归树，你会发现存在「大量重复计算」，比如f（8）被计算了两次，f（7）被重复计算了3次...所以这个递归算法低效的原因，就是存在大量的重复计算！
「那么，怎么解决这个问题呢？」
既然存在大量重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去「备忘录」查一下，如果有，就直接取就好了，备忘录没有才再计算，那就可以省去重新重复计算的耗时啦！这就是「带备忘录的解法」
我们来看一下「带备忘录的递归解法」吧~
一般使用一个数组或者一个哈希map充当这个「备忘录」。
假设f(10)求解加上「备忘录」，我们再来画一下递归树：
「第一步」，f（10）= f(9) + f(8)，f(9) 和f（8）都需要计算出来，然后再加到备忘录中，如下：

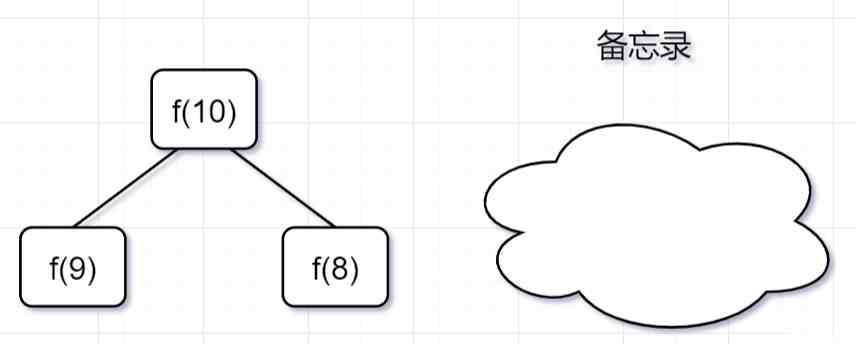
「第二步，」 f(9) = f（8）+ f（7），f（8）= f（7）+ f(6), 因为 f(8) 已经在备忘录中啦，所以可以省掉，f(7),f（6）都需要计算出来，加到备忘录中~

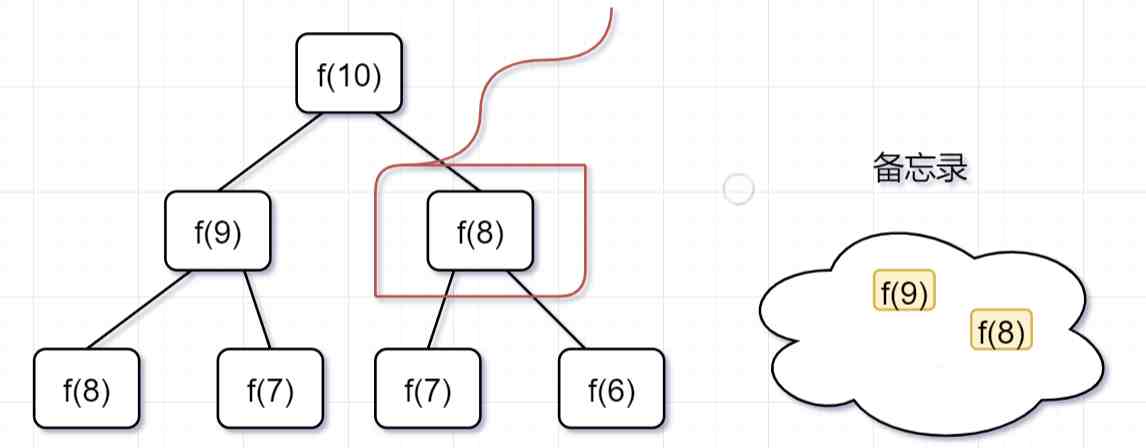
「第三步，」 f(8) = f（7）+ f(6),发现f(8)，f(7),f（6）全部都在备忘录上了，所以都可以剪掉。