一次函数的应用|八年级数学一次函数的应用( 二 )

当通话时间在 400 分钟时，应使用通话方式 ① 比较合算。
3、典型例题
某化妆品公司每月付给销售人员的工资有两种方案：
方案1：没有底薪，只拿销售提成；
方案2：底薪加销售提成。
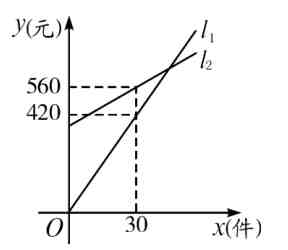
已知每件商品的销售提成方案2 比方案1 少 7 元，设销售人员每月销售 x （件）商品时的月工资为 y （元），如图所示，
L1 表示方案 1 中 y 与 x 之间的函数图像，L2 表示方案 2 中 y 与 x 之间的函数图像。

图（6）
（1）求 L1 所表示的函数关系式；
（2）求方案 2 中每月付给销售人员的底薪是多少元？
（3）当销售数量为多少时，两种工资方案所得到的工资数额相等？
解：
（1） L1 所表示的函数关系式为 y1 = 14x。
（2）因为每件商品的销售提成方案2 比方案1 少 7 元，所以 y2 = ( 14 - 7 ) x + b ,
把（30，560 ）代入得，560 = 730 + b，解得 b = 350，
所以方案 2 中每月付给销售人员的底薪是 350 元。
（3）由题意得：方案1 每件的提成是 42030 = 14 （元），所以方案2 每件的提成是 14 - 7 = 7 （元）。
设销售 m 件时两种工资方案所得到的工资数额相等，由题意得，14m = 350 + 7m , 解得 m = 50。
当销售数量为 50 件时，两种工资方案所得到的工资数额相等。

一次函数的应用|八年级数学一次函数的应用( 二 )

【一次函数的应用|八年级数学一次函数的应用】