神经网络控制|神经网络智能控制系统的研发( 三 )

表1控制策略组态元件图标元件名称元件功能中间模拟量模拟量输入输出的中间值模拟量设定器产生模拟量信号SIN发生器产生正弦信号比例调节器输入与比例相乘后的数值加法运算器输出等于两个输入的累加乘法运算器输出等于两个输入信号相乘除法运算器输出等于两个输入信号相除
5仿真实验结果
本实验中，设置学习率c=003，I=002，IAPsimu虚拟控制站的计算周期T1=100 ms，上位机中数据监控周期T=500 ms 。仿真实验结果分别如图5~7所示。

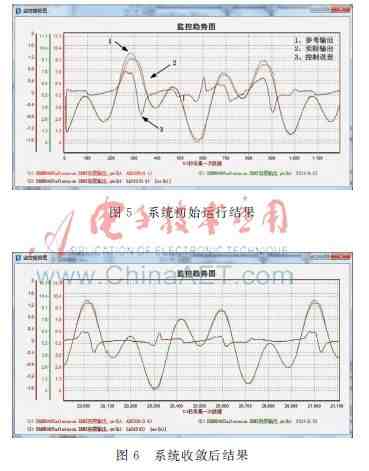
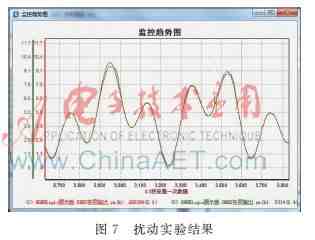
图5所示是神经网络智能控制系统开始运行（计算）10 min内的仿真结果。图中三条曲线分别表示参考输出yr(k)、设备的实际输出y(k)与控制误差ec(k)=yr(k)－y(k) 。可以看出，在初始计算的10 min之内，设备实际输出y(k)在上升和下降阶段拟合参考输出yr(k)的情况较好，但在参考输出yr(k)的波峰及波谷处仍有较大误差，控制误差ec(k)最大值为07 。
图6是控制系统收敛后的结果，从图中可看出，在参考输出yr(k)的波峰及波谷处误差明显减小，此时控制误差ec(k)的最大值已从初始运算时的07下降到03 。
在神经网络智能控制系统稳定的情况下，加入赋值为1、持续时间为5 s的扰动信号，系统的调整曲线如图7所示。百思特网图中可以看出，虽然控制系统受到较大干扰，但系统有较好的自调节、自适应能力，能迅速恢复到稳定状态。
6结论
本文采用图形化、常规控制的控制策略组态元件来构建神经网络智能控制系统，组态方法简单、便捷，成功地将对角递归神经网络的先进控制算法与常规控制算法的图形化组态集成在同一个计算环境中。系统运行时，元件计算过程可观测、可操控，还能够以动态趋势图形显示的形式将神经网络的学习特性展示出来，有效地降低了神经网络控制系统的复杂性，极大地缩短了控制系统开发和部署的时间。系统计算过程透明、可观测，系统中所有权值、变量数据可自动记录在计算机中，供技术人员分析对角递归神经网络系统控制品质使用，方便了智能控制算法在工业控制系统中的实施。
参考文献
［1］ KU C C, LEE K Y. Diagonal recurrent neural networks for dynamic systems control［J］. IEEE Transaction on Neural Networks,1995, 6(1):144-156.
［2］戴晟. 基于DE算法的DRNN网络非线性系统辨识研究［D］. 成都：西南交通大学，2011.
［3］姚庆文，何成平. 基于自适应PID的切带机控制系统设计［J］. 煤炭技术，2011，30(11)：45-47.
［4］陈大明. 基于对角递归神经网络永磁同步电机无传感器控制研究［D］. 沈阳：沈阳工业大学，2007.
［5］陈冲，胡国文，刘星桥，等. 基于DRNN的三电机变频调速系统参数PID控制研究［J］. 盐城工学院学报(自然科学版)，2010，23(3)：39-43.