误差分析|如何正确地做误差分析( 三 )

那么，第二条原则可以正式地表述为：错误出现频率的分析应该在整个数据集上进行，其中需要包括正例（true positive）。

原则 3：测试错误猜想，验证因果性现在我们已经建立起关于干扰词的分组了。但是，出现错误的时候同时有一个干扰词并不一定代表干扰词是这个错误出现的根本原因。回到前面的例子，我们可以简单地认为出错的根本原因是因为有干扰词，但也可能是因为我们需要做多句推理，需要把「神秘博士」和「系列」联系起来，又或者还有别的原因。

这就引出了我们当前面对的百思特网现状中的另一个问题：我们很难有效地分离某个错误的根本原因。想要弄清的话，我们需要第三个原则
原则 3：错误猜想要经过显式的测试验证
借助 Errudite ，论文作者们想要回答这个问题：这 192 个错误都是因为有干扰词才出错的吗？验证方法是提出并验证一个相关的假想问题：「如果没有这个干扰词，模型能不能给出正确的答案？」作者们利用重写规则，用反事实分析（counterfactual analysis）寻找答案。
根据这个领域专用语言， Errudite 可以按一定的规则重写分组内的所有实例。比如在这里，为了验证干扰词是否是根本原因，根据重写规则把文本中的干扰词都替换成无意义的占位符「#」，这样就不会再被检测为实体。
在重写完成以后让模型重新进行预测。在前面那个神秘博士的例子里，即便已经用「#」替换了错误答案 John Debney ，模型仍然给出了另一个错误答案 Ron Grainer 。看来另一个干扰词仍然迷惑了模型。
对于分组中的其它样本，有 29% 的情况模型会给出另一个不正确的同类型实体（另一个干扰词）；在 48% 的情况中，模型给出了正确的预测，这部分样本里确实是干扰词带来了错误预测；在剩下的 23% 中，模型给出了和之前相同的预测 —— 只不过由于现在那些字符已经被「#」替换，所以模型的预测结果就会包含这个没有任何实际含义的「#」字符！可以猜测这可能是因为问题和预测答案高度重合，所以模型实际做的更接近于直白的字符匹配而不是寻找实体。从这种反事实分析中得到的结论就不是仅仅做一下分组就能得到的了。

准确 + 可重现 + 可重复应用在上面这个误差分析过程中，我们需要用准确的查询语句构建属性、分组，以及执行重写规则。对 BiDAF 进行分析过后，我们发现有干扰词的时候它的表现并不怎么差，而且一些以前我们以为是干扰词引起的问题其实有其它的根本原因。
此外，准确的查询语句有一个非常大的好处，就是可以轻松地分享给他人、重现实验结果，以及其它的模型乃至其它的任务中应用。
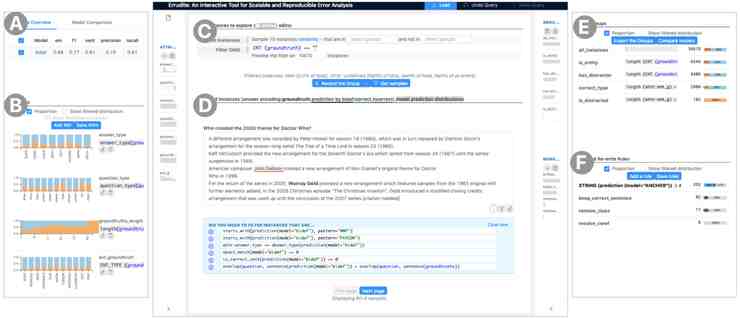
最后，论文作者们还表示这个 Errudite 工具有一个明了、易用、多功能的图形化用户界面，而且带有语句示范、属性分布图等实用功能。

要点总结常见（但有偏倚的）误差分析来自于
主观的错误分组 + 小样本 + 只关注错误情况 + 没有针对根本原因的测试
Errudite（改进的）误差分析
准确、可重复的分组 + 分析整个数据集 + 包含了正例和负例 + 通过反事实分析测试验证

NLP 领域之外的误差分析的启示目前的 Errudite 实现（尤其是其中的领域专用语言部分）只是针对 NLP 任务的。然而，机器学习系统也经常需要处理非文本数据。论文作者们相信，即便目前他们的实现难以拓展到其它的领域，但他们的三条原则，完全可以、也完全有必要在其他的领域中得到应用，帮助大家部署正确的模型、向正确的研究方向深入挖掘。
想要创建一个新的基于这三条原则的工具并不难，只需要它可以支持对应的这三个要点：
运用领域专用语言，通过可编辑修改的基础部件，完成准确的样本分组；
拓展误差分析规模，通过自动的过滤语句分析包括正例和负例在内的所有样本，并提供可视化的统计数据；