所以 ， 我们可以这样理解dx：“将原本用短条宽度x计算的数值 ， 看作趋向于0的‘精确值’ 。”
总结一下 ， 德尔塔（）和英文小写字母d分别在以下情况中使用 。
德尔塔（）——当存在宽度（宽度大于0）之时 。
英文小写字母d——当宽度趋向于0 ， 计算极限数值时 。
另外 ， 虽然微积分中会出现各种各样的公式、符号 ， 不过初学者最开始不太理解这些东西也没有关系 ， 对和d也同样如此 。
感觉和逻辑初中入学考试中的积分
我们来思考两方面内容：“有效分割图形的方法”和“积分符号的使用方法” 。为了便于讲解 ， 我选取了初中入学考试试题 ， 并尝试使用积分方法解答 。
下面 ， 我们将接触到旋转体 。旋转体的体积是日本高中教科书中必定会出现的内容 ， 初中入学考试中则常常会出现简单的旋转体题目 ， 例如下面的题目 。



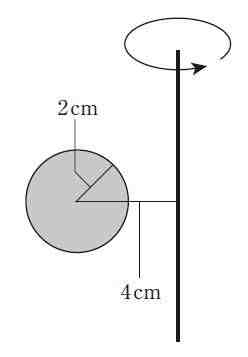
如图所示 ， 存在一个半径为2 cm的圆板 ， 距离该圆板圆心4 cm处存在一条竖轴 ， 让圆板以竖轴为轴旋转一周 ， 求出此时所形成的图形的体积 。

题目出自日本东海大学附属高轮台高等学校中等部2007年入学考试试题 ， 内容表述有部分修改 。

该如何解答这个问题？



圆板绕轴旋转一周 ， 这时会变成什么样的图形呢？



如图43所示 ， 圆板旋转后就变成了这种甜甜圈形 。这种甜甜圈的形状在数学中被称作圆环体 。
为了计算出圆环体的体积 ， 我们来寻找最朴素的“积分”法 。那什么样的方法最有效呢？
如图44所示 ，  我们可以考虑从水平方向切割圆环体 。



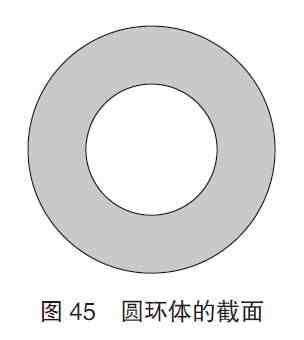
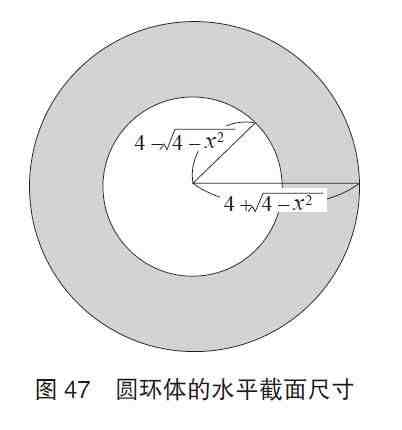
如图45所示 ， 切割圆环体所得的截面如同从一个大圆中挖去了一个同心的小圆 。求截面面积的话 ， 只要知道大圆和小圆的半径就可以了 。计算方法和计算钵体截面面积时的相同 。



难点在于 ， 圆的半径该如何计算呢？
下面来尝试将我们的思路画到题目给出的图中 。取旋转轴为x轴 ， 并将各个点标注上字母（图46） 。
在x轴取点H 。这样一来 ， 图45截面上的两个圆 ， 大圆的半径为AH ， 小圆的半径为BH 。



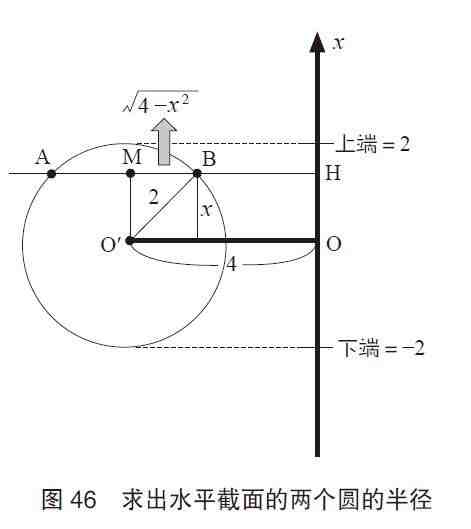
实际上 ， 我们的思路中最关键的一点在于“用H的高度去切割圆环体” 。着眼于这点就可以发现：我们可以使用勾股定理 。
接着 ， 设点A、点B的中点为M 。这时 ， 根据勾股定理可知 ， AM（BM）的长为根号下4?x2 。也就是说 ， 大圆的半径AH为



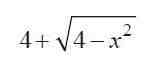
小圆的半径BH为









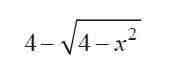
具体的计算过程在此省略 。
圆环体的体积可以看作是 ， 在从下面（x=?2）到上面（x=2）的范围内 ， 众多厚度为x的截面积（薄切片）的组合（截面积之和） 。使用积分符号 ， 可以用如下表示：



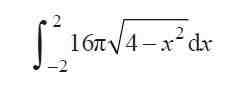
这样一来 ， 我们就求出了圆环体的体积 。



我们来思考一下这个式子中“有意义的部分” 。从整体结构看 ， 16可以最后乘进去 ， 所以可以先不管它 。首先应该求的部分是






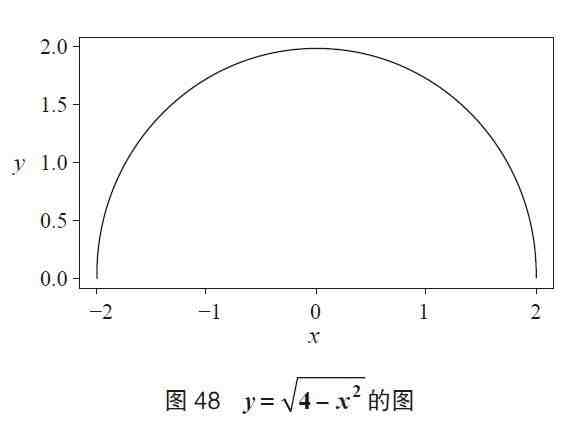
但是 ， 这种办法并非能轻易想到 。所以 ， 在目前的阶段 ， 大家可不必过分在意 ， 先继续往下读 。

• 马鞍山|2020马鞍山历年常住人口一览 马鞍山各区县人口排行榜
• 呼和浩特|2020呼和浩特各区县人口排行 呼和浩特历年常住人口数
• 商丘|2020商丘各区县人口排行榜 商丘市历年常住人口数
• 淄博|2020淄博各区县人口排行 淄博市历年常住人口数量
• 秦皇岛|2020秦皇岛各区县人口排行 秦皇岛历年常住人口数
• 绵阳|2020绵阳各区县人口排行榜 绵阳历年常住人口数一览
• 乌鲁木齐|2019乌鲁木齐各区县人口排行 乌鲁木齐历年常住人口数一览
• 鹤岗|2020鹤岗历年总人口数一览 鹤岗各区县人口排行榜
• 诺贝尔奖|历年诺贝尔生理学或医学奖得主名单 诺贝尔生理学或医学奖历年得主和成就
• 诺贝尔奖|历年诺贝尔物理学奖得主名单 诺贝尔物理学奖历年得主和成就