也就是说 ， 图51中画粗线的圆的半径为82-1.5=2.5 cm 。因此 ， 甜甜圈的体积等于底面积为1.5、高为22.5 cm的圆柱的体积 ， 即为



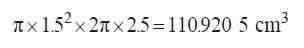
这大概和棱长为4.8 cm的立方体体积相当 。
帕普斯—古尔丁定理
在日本中学的入学考试中 ， 存在一个求旋转体体积的“秘技”——帕普斯—古尔丁定理 。



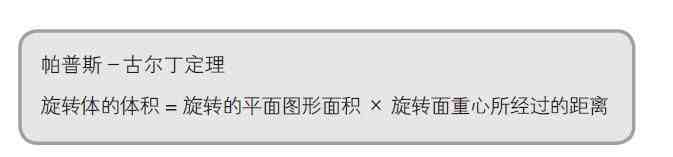
下面我们使用这个定理计算旋转体的体积 。
在前面的圆环体中 ， “旋转的平面图形”是半径为2的圆 ， 其面积为22=4 。
接着是“旋转面重心所经过的距离” ， 这道题里的“重心”大家可以理解为是“旋转体的正中央” 。重心经过的距离等同于圆柱的高 ， 所以是42=8 。
把这些数据代入帕普斯—古尔丁定理 ， 可得“旋转体的体积”为48=32 。
不少机灵的小学生都知道这个“秘技” ， 在实际的考试中肯定也有考生使用这个定理 。但是 ， 真正要来解释这个计算原理 ， 如大家所见 ， 还真不是一件容易的事情 。
将圆环体变形成圆柱 ， 我们可以从这个过程中窥得积分的要领 。



实际上 ， 使用相同的方法也可以计算圆环体的“表面积” 。
在图55中能够确认 ， 圆环体的表面积等于“底面半径为2、高为8的圆柱的侧面积” 。因此 ， 半径为2的圆的周长为22=4 ， 再乘以8 ， 则圆环体的表面积就等于32 。顺便说一下 ， 这里的表面积和体积相等（都是32） ， 只是一个偶然 。
另外 ， 使用将圆环体变形为圆柱的方法 ， 也能轻松推导出圆环体的体积和表面积的公式 。



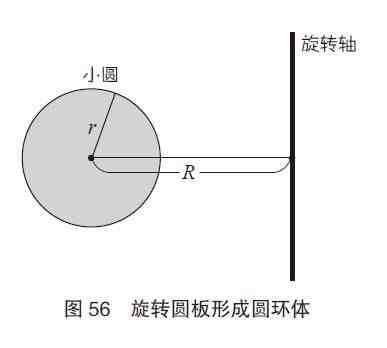
如图56所示 ， 取r和R（R＞r）使之围绕轴旋转形成圆环体 。将半径为r的灰色圆板称为小圆 ， 则圆环体的体积和表面积的公式如下：
体积=小圆的面积（r）小圆圆心经过的距离（2R） =2rR
表面积=小圆的周长（2r）小圆圆心经过的距离（2R）=4rR
表面积的这种计算方法只要理解了就会觉得非常简单 ， 但若使用其他计算方法就会比较麻烦 ， 需要用到多重积分这种大学水平的积分知识 。分割方法 ， 让积分可易可难 。
反过来说 ， 那些看起来复杂困难的问题 ， 仅仅通过分割的方法 ， 就能转化为小学生也可以解开的问题了 。
积分在应用时 ， 数值计算多会使用计算机来处理 。实际上 ， 把具体的积分式子写出来并计算的情况少之又少 。计算机计算积分问题 ， 除了技术上的运行处理外 ， 剩下其实都是在“求取所有分割面积（或者长度、体积）的总和” 。
说到底 ， 积分可以说就是求取“分割部分之和” ， 并无其他特别内容 。一旦可以写出积分的式子 ， 那么数值计算就很简单了 。
将各种各样的量用积分的式子表达出来 ， 这才是我们需要掌握的必要能力 。
——本文选自《简单微积分：学校未教过的超简易入门技巧》



书中以微积分的“思考方法”为核心 ， 以生活例子通俗讲解了微积分的基本原理、公式推导以及实际应用意义 ， 解答了微积分初学者遭遇的常见困惑 。没有烦琐计算、干涩理论 ， 是一本只需“轻松阅读”便可以理解微积分原理的入门书 。
第1章 积分是什么
积分的存在意义
两个思想实验
切口的秘密
感觉和逻辑
第2章 微分是什么
微分存百思特网在的意义
丰富多彩的函数世界
有预谋地使用微分
第3章 探寻微积分的可能性
1800年后的真相
填坑
弯曲也没问题
微积分的真身
点击【了解更多】跳转到京东购买